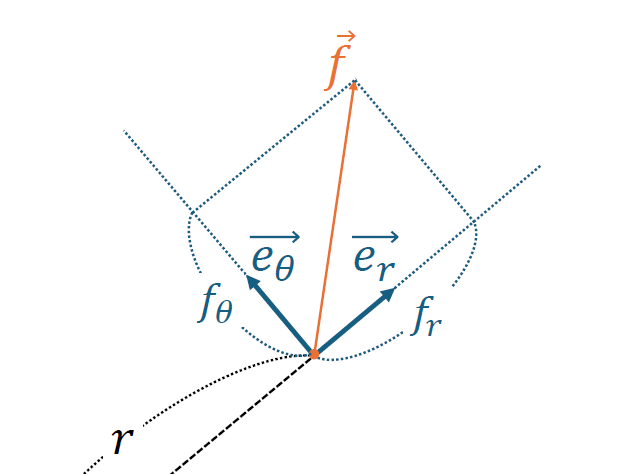
今まで、極座標を使った計算に苦手意識を覚えていた。最近になってようやく少しだけ真面目に勉強したところ、理解を妨げる原因を特定できた。そこで本記事では、現時点での自分の理解を整理したい。
定義
2次元極座標では、平面上のある座標を、動径と偏角の組$(r,\theta)$で表す。そして、座標$(r,\theta)$上で観測されるベクトル量$\vec{f}$を、その座標における動径方向と方位角方向の2成分に分解し、
$$\vec{f} = f_r \vec{e_r} + f_\theta \vec{e_\theta}\label{1}\tag{1}$$
と表す。
ここで、注意しなければならないことは次の2点である。
1点目は、$(r,\theta) \neq r \vec{e_r} + \theta \vec{e_\theta}$であることだ。直交座標では$(x,y)$と$x \vec{e_x} + y \vec{e_y}$を混同していても大きな問題にならないが、極座標ではこれを明確に区別しなければならない。
2点目は、$\vec{e_r}$と$\vec{e_\theta}$は$\theta$の関数であることだ。座標ごとに基底ベクトルの向きが異なるという性質が、直交座標系と比べて諸々の議論をややこしくしていると言ってよい。
直交座標と極座標の変換
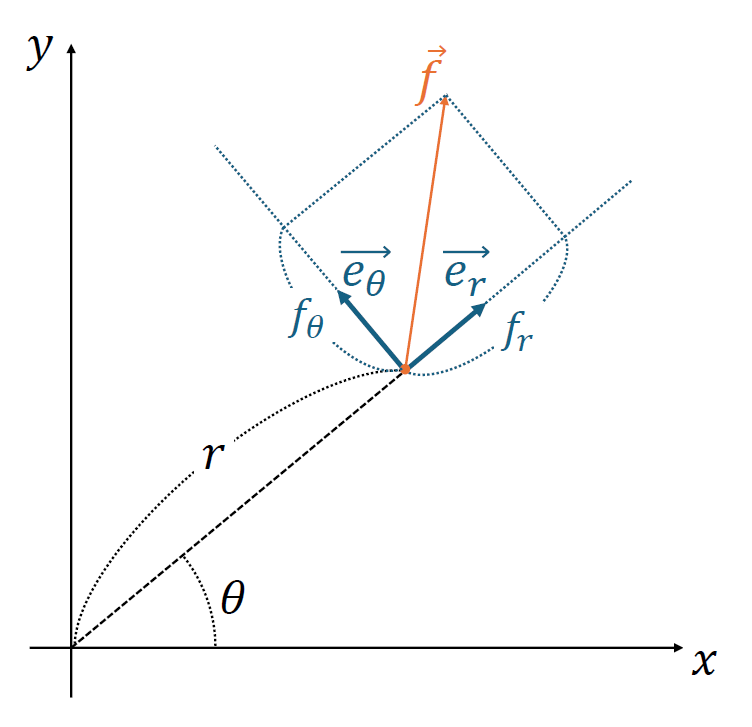
先ほどの図1より、
$$\begin{align}x&=r \cos\theta\label{2}\tag{2} \\ y &= r \sin\theta\label{3}\tag{3} \end{align}$$
と分かる。これを逆解きすれば、
$$\begin{align}r&=\sqrt{x^2+y^2}\label{4}\tag{4} \\ \theta &=\arctan\left(\frac{y}{x}\right)\label{5}\tag{5} \end{align}$$
となる。
基底ベクトルの変換についても、図1より、
$$\begin{align}\vec{e_r} &= \cos\theta \cdot \vec{e_x} + \sin\theta \cdot \vec{e_y}\label{6}\tag{6}\\\vec{e_\theta} &= -\sin\theta \cdot \vec{e_x} + \cos\theta \cdot \vec{e_y}\label{7}\tag{7}\end{align}$$
であり、逆解きして、
$$\begin{align}\vec{e_x} &= \cos \theta \cdot \vec{e_r} – \sin \theta \cdot\vec{e_\theta}\label{8}\tag{8} \\\vec{e_y} &= \sin\theta\cdot\vec{e_r} + \cos\theta\cdot\vec{e_\theta}\label{9}\tag{9}\end{align}$$
となる。
また、(\ref{6}), (\ref{7})式を$\theta$で偏微分することで、
$$\begin{align}\frac{\partial \vec{e_r}}{\partial \theta} &= \vec{e_\theta}\label{10}\tag{10} \\ \frac{\partial \vec{e_\theta}}{\partial \theta} &= -\vec{e_r}\label{11}\tag{11}\end{align}$$
を得る。先ほど述べた通り、2次元極座標系の基底ベクトルの向きは$\theta$とともに変化する。(\ref{10}), (\ref{11})式を「常識」にしておくことが、極座標絡みの計算で混乱しないために重要である。
極座標におけるベクトル微分演算子$\nabla$の表示
直交座標における定義は
$$\nabla = \vec{e_x}\frac{\partial}{\partial x} + \vec{e_y}\frac{\partial}{\partial y}\label{12}\tag{12}$$
である。
言うまでもないが、演算子(operator)を考える上では、被演算子(operand)の存在を忘れてはならないことに注意が必要だ。先ほどの(\ref{12})式は、例えば次のように被演算子となるスカラー量$f$とともに
$$\nabla f = \vec{e_x}\frac{\partial f}{\partial x} + \vec{e_y}\frac{\partial f}{\partial y}\label{13}\tag{13}$$
と用いられることを頭に入れておかねばならない。
(\ref{13})式を2次元極座標系へ変換してみよう。(\ref{8}), (\ref{9})式、および連鎖律を用いることで、
$$\begin{align}\nabla f = &(\cos \theta \cdot\vec{e_r} – \sin \theta \cdot\vec{e_\theta})\left(\frac{\partial r}{\partial x}\frac{\partial f}{\partial r} + \frac{\partial \theta}{\partial x}\frac{\partial f}{\partial \theta}\right) \\ &+ (\sin\theta\cdot\vec{e_r} + \cos\theta\cdot\vec{e_\theta})\left(\frac{\partial r}{\partial y}\frac{\partial f}{\partial r} + \frac{\partial \theta}{\partial y}\frac{\partial f}{\partial \theta}\right) \label{14}\tag{14}\end{align} $$
とできる。ここで、(\ref{4}), (\ref{5})式より、
$$\begin{align}\frac{\partial r}{\partial x} &= \cos \theta \\ \frac{\partial r}{\partial y} &= \sin \theta \\ \frac{\partial \theta}{\partial x}&=-\frac{\sin\theta}{r} \\ \frac{\partial \theta}{\partial x}&=\frac{\cos\theta}{r}\end{align}$$
である。これらを(\ref{14})式に代入して、
$$\begin{align}\nabla f = &(\cos \theta \cdot\vec{e_r} – \sin \theta \cdot\vec{e_\theta})\left(\cos \theta\cdot\frac{\partial f}{\partial r} -\frac{\sin\theta}{r}\cdot\frac{\partial f}{\partial \theta}\right) \\ &+ (\sin\theta\cdot\vec{e_r} + \cos\theta\cdot\vec{e_\theta})\left(\sin \theta\cdot\frac{\partial f}{\partial r} + \frac{\cos\theta}{r}\cdot\frac{\partial f}{\partial \theta}\right) \\ =& \vec{e_r}\frac{\partial f}{\partial r} + \vec{e_\theta}\frac{1}{r}\frac{\partial f}{\partial \theta} \label{15}\tag{15}\end{align} $$
となる。被演算子である$f$を省いて書けば、
$$\nabla = \vec{e_r}\frac{\partial }{\partial r} + \vec{e_\theta}\frac{1}{r}\frac{\partial }{\partial \theta}\label{16}\tag{16}$$
となる。
極座標における発散(div)と回転(rot)の表示
前述の方法と同様に真面目に変換することで、極座標における発散や回転の表示も得られるはずである。しかし少々面倒であるから、今回は(\ref{16})式を利用してこれらの表示を計算することを考える。
被演算子となるベクトル量$\vec{f} = f_r \vec{e_r} + f_\theta \vec{e_\theta}$を用いて、
$$\begin{align}\nabla \cdot \vec{f} =& \left(\vec{e_r}\frac{\partial }{\partial r} + \vec{e_\theta}\frac{1}{r}\frac{\partial }{\partial \theta}\right)\cdot ( f_r \vec{e_r} + f_\theta \vec{e_\theta}) \\ =& \frac{\partial f_r}{\partial r} \vec{e_r}\cdot\vec{e_r}+ f_r\vec{e_r}\cdot\frac{\partial \vec{e_r}}{\partial r} +\frac{\partial f_\theta}{\partial r} \vec{e_r}\cdot\vec{e_\theta}+ f_\theta\vec{e_r}\cdot\frac{\partial \vec{e_\theta}}{\partial r} \\ &+\frac{1}{r}\frac{\partial f_r}{\partial \theta} \vec{e_\theta}\cdot\vec{e_r}+ \frac{f_r}{r}\vec{e_\theta}\cdot\frac{\partial \vec{e_r}}{\partial \theta} +\frac{1}{r}\frac{\partial f_\theta}{\partial \theta} \vec{e_\theta}\cdot\vec{e_\theta}+ \frac{f_\theta}{r}\vec{e_\theta}\cdot\frac{\partial \vec{e_\theta}}{\partial \theta}\\ =& \frac{\partial f_r}{\partial r}+ \frac{f_r}{r}+\frac{1}{r}\frac{\partial f_\theta}{\partial \theta} \label{17}\tag{17}\end{align}$$
となる。ただし、最後の式変形で(\ref{10}), (\ref{11})式を用いた。
なお(\ref{17})式は次のように表されることが多い。
$$ \nabla \cdot \vec{f} = \frac{1}{r}\frac{\partial}{\partial r} \left(r f_r\right)+\frac{1}{r}\frac{\partial f_\theta}{\partial \theta} \label{18}\tag{18}$$
同様にして、
$$\begin{align}\nabla \times \vec{f} =& \left(\vec{e_r}\frac{\partial }{\partial r} + \vec{e_\theta}\frac{1}{r}\frac{\partial }{\partial \theta}\right)\times ( f_r \vec{e_r} + f_\theta \vec{e_\theta}) \\ =& \frac{\partial f_r}{\partial r} \vec{e_r}\times\vec{e_r}+ f_r\vec{e_r}\times\frac{\partial \vec{e_r}}{\partial r} +\frac{\partial f_\theta}{\partial r} \vec{e_r}\times\vec{e_\theta}+ f_\theta\vec{e_r}\times\frac{\partial \vec{e_\theta}}{\partial r} \\ &+\frac{1}{r}\frac{\partial f_r}{\partial \theta} \vec{e_\theta}\times\vec{e_r}+ \frac{f_r}{r}\vec{e_\theta}\times\frac{\partial \vec{e_r}}{\partial \theta} +\frac{1}{r}\frac{\partial f_\theta}{\partial \theta} \vec{e_\theta}\times\vec{e_\theta}+ \frac{f_\theta}{r}\vec{e_\theta}\times\frac{\partial \vec{e_\theta}}{\partial \theta}\\ =&\left( \frac{\partial f_\theta}{\partial r}-\frac{1}{r}\frac{\partial f_r}{\partial \theta}+\frac{f_\theta}{r}\right) \vec{e_r}\times \vec{e_\theta}\label{19}\tag{19}\end{align}$$
となる。こちらに関しても、
$$ \nabla \times \vec{f} = \left[\frac{1}{r}\frac{\partial}{\partial r} \left(r f_\theta\right)-\frac{1}{r}\frac{\partial f_r}{\partial \theta}\right] \vec{e_r}\times \vec{e_\theta} \label{20}\tag{20}$$
のように表されることが多い。