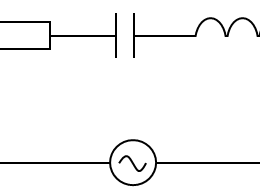
個別指導塾で講師をしていると、交流回路について質問を受けることが多くある。そこで本記事では、普段生徒に交流回路をどう教えているかを書き留めることにする。
交流回路の基本的な考え方
交流回路に関する問題は強制振動と呼ばれる現象に区分される。強制振動とは、「強制的に引き起こされる振動現象」のことである。身近な例として、縁日で見かけるヨーヨーが挙げられる。手を上下させることでヨーヨーを強制的に振動させているわけだから、これは強制振動の一種と言える。同様に交流回路も「回路に正弦波電圧を与えることで、振動電流を強制的に生じさせる」ものだから、強制振動の一種といえる。
強制振動に関する問題では、特に次の2点が興味の対象となる。
- 与える振動の(角)振動数に対して、運動の振幅はどれほどか
- 与える振動の位相に対して、運動の位相のずれはどれほどか
前者について、振幅の大きな運動の実現される場合を共振(共鳴)とよぶ。共振は、例えば長周期地震動による高層ビルの大きな揺れや、ラジオの選局回路の原理であって、実用上きわめて重要な概念といえる。
【広告】chocoZAP
本サイトの管理人も週2で通っているchocoZAPの紹介です。着替え不要・シューズ履き替え不要で、隙間時間にサッとトレーニングすることができます。
抵抗のみの場合
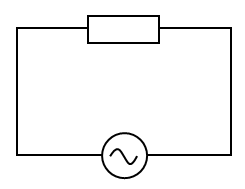
もっとも簡単な例として、交流電源に抵抗$R$のみを繋いだ場合を考える。交流電源の電圧を
$$
V = V_0 \sin \omega t
$$
とすると、オームの法則$V=RI$より電流は
$$
I = \frac{V_0}{R} \sin \omega t
$$
となる。電流の最大値$I_0$は$I_0 = V_0/R$と分かる。
回路の電力$P$は$P=VI$と計算でき、
$$
P = \frac{V_0^2}{R}\sin^2 \omega t
$$
ゆえ、回路の平均電力$\bar{P}$は
$$
\begin{align}
\bar{P} &= \int_0^{2\pi / \omega} \frac{V_0^2}{R}\sin^2 \omega t \rm{d}t \\
&= \frac{V_0^2}{2R}
\end{align}
$$
である。
ここで、新しい量として
$$
\begin{align}
V_e &= \frac{V_0}{\sqrt{2}} \\
I_e &= \frac{V_e}{R} \left( = \frac{I_0}{\sqrt{2}}\right)
\end{align}
$$
を定義すると、回路の平均電力$\bar{P}$の式を
$$
\bar{P} = \frac{V_e^2}{R} = V_e I_e
$$
と書き換えられる。この式は直流での電力の公式と対応付けでき、またそうなるように定義された$V_e,I_e$をそれぞれ実効電圧、実効電流とよぶ。
コンデンサーのみの場合
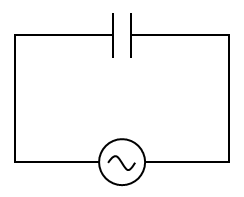
続いて、交流電源をコンデンサー$C$に繋いだ場合を考える。コンデンサーに蓄えられた電気量$Q$は、コンデンサーの両端の電位差$V_C$(時計回りの向きに電位降下する場合を正とする)および電気容量$C$を用いて
$$
Q=CV_C
$$
と表される。また、電流の定義(単位時間当たりの電荷の流れ)より、(時計回りの流れを正として)
$$
I = \frac{\rm{d}Q}{\rm{d}t}
$$
である。
よって、キルヒホッフの第二法則より
$$
\begin{align}
V_0 \sin \omega t &= V_C \\
V_0 \sin \omega t &= \frac{Q}{C}
\end{align}
$$
ここで、両辺を$t$で微分して
$$
\begin{align}
\omega V_0 \cos \omega t &= \frac{1}{C}\frac{\rm{d}Q}{\rm{d}t} \\
\omega V_0 \cos \omega t &= \frac{1}{C}I \\
I &= \omega C V_0 \cos \omega t \\
&\left(= \omega C V_0 \sin \left(\omega t + \frac{\pi}{2}\right)\right)
\end{align}
$$
となる。したがって、回路を流れる電流は交流電源の電圧に対し$\pi/2$進んでいるといえる。
電流の最大値$I_0$は$I_0 = \omega C V_0$と分かる。この関係式を変形すると
$$
V_0 = \frac{1}{\omega C} I_0
$$
と書ける。$\displaystyle X_C = \frac{1}{\omega C}$を、コンデンサーのリアクタンスとよぶ。リアクタンスの記号を用いれば、上式は
$$
V_0 = X_C I_0
$$
とオームの法則の形のように表せる。リアクタンスは、いわば「交流回路における抵抗値」のようなものといえる。
ただし、コンデンサーでの平均電力は$0$である点に注意が必要である。実際、
\begin{align}
\bar{P} &= \int_0^{2\pi / \omega} \omega C V_0^2 \sin \omega t \cos \omega t \rm{d}t \\
&= 0 \quad(\because 三角関数の直交性)
\end{align}
となる。コンデンサーは抵抗と異なり、時間平均を取ると電力消費は$0$なのである。
コイルのみの場合
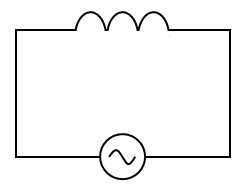
交流電源をインダクタンス$L$のコイルに繋いだ場合を考える。コイルに時間変動する電流を流すと、逆起電力
$$
E_L = -L\frac{\rm{d}I}{\rm{d}t}
$$
が生じる。これと電源電圧$V$の和が打ち消し合うので、
$$
\begin{align}
V + E_L &= 0 \\
V_0 \sin \omega t -L\frac{\rm{d}I}{\rm{d}t} &= 0
\end{align}
$$
と書ける。
コイルに生ずるのは逆「起電力」であるから、その意味合いを重視するならば上記のように左辺に$E_L$を書くべきである。しかし計算上、コイルを「交流回路における抵抗器のようなもの(厳密にはインダクタとよぶ)」とみなしてキルヒホッフの第二法則の式を立てた方が便利である。そこで、コイルを両端の電位差が
$$
V_L = -E_L
$$
である抵抗器のようなものとみなして
$$
\begin{align}
V &= V_L \\
V_0 \sin \omega t &= L\frac{\rm{d}I}{\rm{d}t}
\end{align}
$$
と立式することが多い。コイルについて立式するときマイナスの符号をつけるかどうか迷う人が多いが、上記の議論が参考になるはずだ。
本題に戻り、先ほどの式を$t$で積分して整理すると、
$$
\begin{align}
– \frac{V_0}{\omega} \cos \omega t &= LI \\
I &= – \frac{V_0}{\omega L} \cos \omega t
\end{align}
$$
となる。したがって、回路を流れる電流は交流電源の電圧に対し$\pi/2$遅れているといえる。
電流の最大値$I_0$は$\displaystyle I_0 = \frac{V_0}{\omega L}$と分かる。この関係式を変形すると
$$
V_0 = \omega L I_0
$$
と書ける。$\displaystyle X_L = \omega L $を、コイルのリアクタンスとよぶ。コンデンサーの場合と同様に、リアクタンスの記号を用いれば、上式は
$$
V_0 = X_L I_0
$$
とオームの法則の形のように表せる。
また、コンデンサーの場合と同様に計算することで、コイルでの平均電力も$0$であると分かる。
RLC並列回路
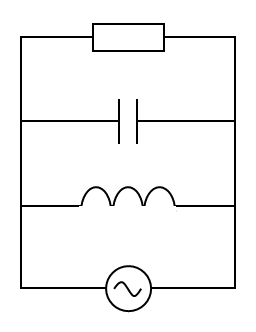
抵抗・コンデンサー・コイルを並列に繋いだ回路(RLC並列回路)を考える。並列回路だから、抵抗・コンデンサー・コイルの両端の電位差は電源電圧と等しく、$V=V_0 \sin \omega t$である。よって、回路を流れる電流の総量(電源に流れる電流)は
$$
\begin{align}
I &= \frac{V_0}{R} \sin \omega t + \omega C V_0 \cos \omega t – \frac{V_0}{\omega L} \cos \omega t \\
&= V_0 \left[ \frac{1}{R} \sin \omega t + \left( \omega C – \frac{1}{\omega L} \right)\cos \omega t \right] \\
&= V_0 \sqrt{\frac{1}{R^2}+ \left( \omega C – \frac{1}{\omega L} \right)^2} \sin (\omega t + \alpha)\\
&\left(ただし、\tan \alpha = R \left( \omega C – \frac{1}{\omega L} \right) である\right)
\end{align} \\
$$
となる。したがって、電源に流れる電流の位相は電源電圧に対し$\alpha$ずれていると分かる。
電流の最大値$I_0$は
$$
\displaystyle I_0 = V_0 \sqrt{\frac{1}{R^2}+ \left( \omega C – \frac{1}{\omega L} \right)^2}
$$
である。この関係式を変形すると
$$
V_0 = \frac{I_0}{\sqrt{\frac{1}{R^2}+ \left( \omega C – \frac{1}{\omega L} \right)^2}}
$$
と書ける。ここで、
$$
\displaystyle Z = \frac{1}{\sqrt{\frac{1}{R^2}+ \left( \omega C – \frac{1}{\omega L} \right)^2}}
$$
を、RLC並列回路のインピーダンスとよぶ。インピーダンスの記号を用いれば、上式は
$$
V_0 =Z I_0
$$
とオームの法則の形のように表せる。
$V_0$が一定のとき、$Z$が最小であれば$I_0$は最大をとる。このような$Z$は、
$$
\begin{align}
\left( \omega C – \frac{1}{\omega L} \right)^2 &= 0 \\
\omega = \frac{1}{\sqrt{LC}}
\end{align}
$$
のとき実現する。この場合を共振という。
RLC直列回路
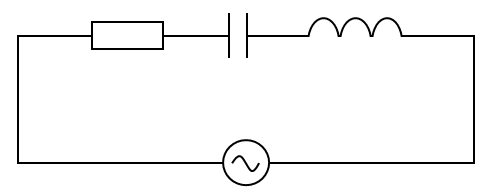
最後に、RLC直列回路の場合を考える。本来であれば、今までの議論の通り「電源電圧$V=V_0 \sin \omega t$を与えたときの振動電流の値」を計算したい。しかしながら直列回路の場合、抵抗・コンデンサー・コイルの両端の電位差の位相が異なるために、初めからそのように考えるのは難しい。
そこで「振動電流$I=I_0\sin \omega t$が流れている場合に電源電圧がどうなっているかを調べる」という方向性で議論を進めることにする。
キルヒホッフの第二法則より、電源電圧$V$と抵抗・コンデンサー・コイルの両端の電位差$V_R,V_C,V_L$の関係は
$$
\begin{align}
V &= V_R + V_C + V_L \\
V &= RI + \frac{Q}{C} + L \frac{\rm{d}I}{\rm{d}t} \\
V &= RI + \frac{1}{C}\int I \rm{d}t + L \frac{\rm{d}I}{\rm{d}t} \\
V &= R I_0\sin \omega t – \frac{I_0}{\omega C} \cos \omega t + \omega L I_0 \cos \omega t \\
V &= I_0 \left[R \sin \omega t + \left(\omega L – \frac{1}{\omega C}\right) \cos \omega t \right] \\
V &= \sqrt{R^2+ \left( \omega L- \frac{1}{\omega C} \right)^2} I_0 \sin (\omega t + \alpha)\\
&\left(ただし、\tan \alpha = \frac{1}{R}\left(\omega L – \frac{1}{\omega C}\right) である\right)
\end{align}
$$
したがって、電源電圧の位相は振動電流に対し$\alpha$ずれていると分かる。
電圧の最大値$V_0$は
$$
V_0 = \sqrt{R^2+ \left( \omega L- \frac{1}{\omega C} \right)^2} I_0
$$
である。
$$
Z = \sqrt{R^2+ \left( \omega L- \frac{1}{\omega C} \right)^2}
$$
を、RLC直列回路のインピーダンスとよぶ。インピーダンスの記号を用いれば、上式は
$$
V_0 = Z I_0
$$
とオームの法則の形のように表せる。
この回路が共振するときは$Z$が最小、すなわち
$$
\omega = \frac{1}{\sqrt{LC}}
$$
のときである(RLC並列回路の場合と同じ!)。
また、上記のキルヒホッフの第二法則の式を
$$
\begin{align}
I_0 &\rightarrow \frac{V_0}{Z} \\
\omega t &\rightarrow \omega t – \alpha
\end{align}
$$
と変換することを考えると、次の関係
$$
\begin{align}
V &= V_0 \sin \omega t \\
I &= \frac{V_0}{Z} \sin(\omega t – \alpha)
\end{align}
$$
を得る。このように変換を施すことで、本来知りたかった形の式を得ることができる(位相差$\alpha$を電流側に押し付けることができる)。
なお直近で、上記の変換を考えることなしに初めからこの形式で求めようとする趣旨の問題が2024年に北海道大学で出題されている。詳細は当該問題の解答を参照してもらいたいが、この場合は電源電圧を$V=V_0\sin\omega t$とした上で、変動電流の解の形を$I = I_0 \sin(\omega t + \alpha)$と仮定した上で$I_0, \alpha$を求めるという流れになる。
まとめ
本記事では、高校生の知っておくべき交流回路の考え方を一通りまとめた。理解するのには一苦労する分、入試では教科書レベルの出題に留まる場合も多く(高校生には出題できない微分方程式の絡む問題となる可能性に気を遣う必要があるため)、得点源にしておくべき分野といえる。本記事が理解の一助となれば幸いである。